Производная и ее приложения
Даем определения производной и дифференциала. Разбираем правила дифференцирования и выводим формулы производных для основных функций. Рассказываем о формуле Тейлора и правиле Лопиталя.
21 материал
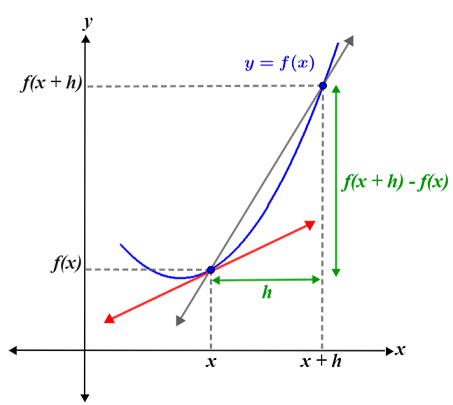
Производная и её физический и геометрический смыслы. Определение производной и дифференциала функции. Односторонние и бесконечные производные.
Расскажем об основных правилах дифференцирования функций. Познакомимся с дифференцированием сложных и параметрических функций. Покажем основные формулы для нахождения производных элементарных функций.
Вторая производная вводится как производная от первой производной. Аналогично вводятся и производные более высоких порядков.
Доказываем ряд теорем для дифференцируемых функций, а именно теоремы Ферма, Ролля, формулу Лагранжа и теорему Коши для конечных приращений.
Формула Тейлора используется для разложение функции в многочлен с остаточными членами в форме Лагранжа и Пеано. Использования формулы Тейлора и Маклорена.
Правило Лопиталя заменяет предел отношения функций пределом отношения их производных, если функции одновременно стремятся к нулю или к бесконечности.